Day 2 - Simplex Projection

class: center, middle, inverse, title-slide

# Day 2 - Simplex Projection
## made simple
### Rafael Lopes
### IFT, Unesp
### 2020-10-28

---

layout: true

background-image:url("logo-IFT.png")
background-position: 0% 100%
background-size: 10%

---
class: left

## Find me at

.left-column[

##### email: rafael.lp.silva@unesp.br
##### Twitter: [@rafalpx](twitter.com/rafalpx)
##### github: [rafalopespx](github.io/rafalopespx)
]
.pull-right[
  ![profile](profile_pick.jpeg)
]
---
## Recapitulando

* Qualquer série temporal pode ser escrita na forma `$X_n=F^n(X_0)$`

* Qualquer sistema dinâmico tem um **espaço-de-fase**

* O **Teorema de Takens** permitir reconstruir espaços-de-fase a partir de uma única série e seus **atrasos**

* Duas **variedades-sombras** que se mapeiam mutuamente, pertencem ao mesmo sistema dinâmico

---
## Questões

* Como determinar o tanto de **atrasos** necessários a reconstrução?

* Como determinar se duas variedades se **mapeiam**?
--
.center[
  Projeção **Simplex** (Hoje)

CCM ou **Convergent Cross Mapping** (Amanhã)
  ]
---
## Projeção Simplex

--
Uma forma de dar uma previsão de curto prazo para uma série temporal é a através de uma projeção simplex, dada uma série temporal:
--
<img src="img/Rplot23.png" width="700" height="475" style="display: block; margin: auto;" />
---
## Projeção Simplex

--
Procuramos o mesmo padrão de logo antes do fim da séries em outros momentos da série, com isso temos:
<img src="img/Rplot24.png" width="700" height="475" style="display: block; margin: auto;" />
---
## Projeção Simplex

--
Com esses padrões olhamos os pontos seguintes, eles nos darão uma ideia do que acontece após esse padrão:
<img src="img/Rplot25.png" width="700" height="475" style="display: block; margin: auto;" />
---
## Projeção Simplex

--
Com esses padrões olhamos os pontos seguintes, eles nos darão uma ideia do que acontece após esse padrão:
<img src="img/Rplot26.png" width="700" height="475" style="display: block; margin: auto;" />
---
## Projeção Simplex

--
Através de uma média ponderada desses padrões podemos estimar o próximo ponto da série, numa fórmula:
$$
\hat{X}(t+h) = \sum^{E+1}_{i=1}w_iX_i(t+h)
$$
--

Ou seja nossa estimativa `$\hat{X}$` será uma média ponderada dos pontos `$X_i$` imediatamente após o padrão
---
## Projeção Simplex

--
Outra forma de visualizar a projeção **Simplex** é através da seguinte ideia, no espaço-de-fase:
<img src="img/simplexextractedf.jpeg" width="700" height="475" style="display: block; margin: auto;" />
---
## Seleção de *Embedding*

--
Para selecionar a dimensão adequada ao **Embedding** contabilizamos a correlação entre o predito e o observado, numa fórmula

$$
`\begin{equation*}
  \rho = \rho_{X,\hat{X}} = \frac{\mathrm{cov}(X,\hat{X})}{\sigma_{X}\sigma_{\hat{X}}} \label{rhosimplex}
\end{equation*}`
$$
Onde `$\rho$` é um valor entre 0 e 1, `$\mathrm{cov}$` é a covariância e `$\sigma$`s são os desvios padrão
---
## Seleção de *Embedding*

Geramos duas séries simples, como abaixo:

```r
## Two vectors to store data
X <- c()
Y <- c()
## Initial values
X[1] <- 0.1
Y[1] <- 0.3
X[2] <- 0.3
Y[2] <- 3.78*Y[1] - 3.78*Y[1]^2
## Iterate the dynamics 150 time steps
for(i in 3:150){
*   X[i] <- 3.77*X[i-1] - 3.77*X[i-1]^2 - 0.85*Y[i-1]*X[i-1] - 0.5*X[i-2]
*   Y[i] <- 3.78*Y[i-1] - 3.78*Y[i-1]^2
}
```
--
$$
`\begin{equation*}
  X_i = 3.77X_{i-1} - 3.77X_{i-1}^2 - 0.85Y_{i-1}X_{i-1} - 0.5X_{i-2} \\
  Y_i = 3.78Y_{i-1} - 3.78Y_{i-1}^2
  \label{eq2sp}
\end{equation*}`
$$

---
## Seleção de *Embedding*

.pull-left[
plotando a série:

```r
plot(X, xlab="Tempo", 
     ylab="X", 
     type="b", 
     lty=3)
```
]
--
.pull-right[
<img src="Day2_Simplex_projection_files/figure-html/unnamed-chunk-8-1.png" width="700" height="400" style="display: block; margin: auto;" />
]
---
## Seleção de *Embedding*

Testamos o `$\rho$` para diferentes dimensões de **embedding**:
.pull-left[

```r
library(rEDM)
*find.emb <- simplex(time_series = X, E = 1:10)
```
]

.pull-right[

```r
head(find.emb$rho, 6)
```

```
## $E1
## [1] 0.2000798
## 
## $E2
## [1] 0.7434791
## 
## $E3
## [1] 0.9220358
## 
## $E4
## [1] 0.9035336
## 
## $E5
## [1] 0.9004385
## 
## $E6
## [1] 0.8682037
```
]
---
## Seleção de *Embedding*
.pull-left[

```r
plot(as.numeric(rho) ~ E, 
     data=find.emb, 
     type="b",
     xlab = "Embedding dimensions",
     ylab = expression(paste("Forecast skill (",rho,")",sep="")))
points(y = find.emb$rho[which.max(find.emb$rho)],
       x = find.emb$E[which.max(find.emb$rho)], 
       col = "red", 
       pch = 19, 
       size = 3)
```
]

.pull-right[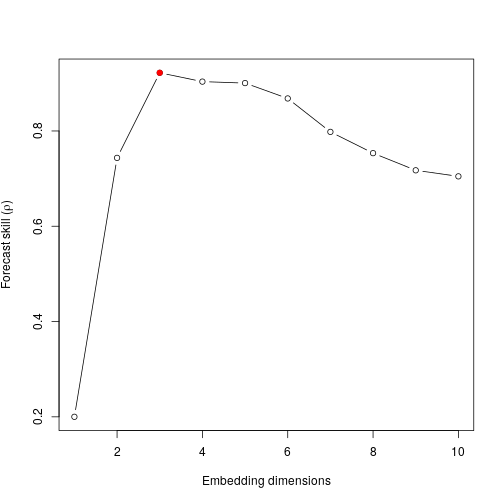
![](Day2_Simplex_projection_files/figure-html/unnamed-chunk-12-1.png)
]
---
## Predições

--
Agora com a dimensão ótima de **embedding** vamos realizar predições:

```r
*predE3 <- simplex(time_series = X, E = 3, stats_only = FALSE)
names(predE3)
```

```
## [1] "stats"        "model_output"
```
--

```r
fits <- predE3$model_output[[1]]
head(fits)
```

```
##   Index Observations Predictions Pred_Variance Const_Predictions
## 1     3    0.5392810         NaN           NaN               NaN
## 2     4    0.5030702   0.3636169  8.193049e-03         0.5392810
## 3     5    0.2915131   0.3533368  2.930746e-03         0.5030702
## 4     6    0.4366629   0.4492918  1.441837e-05         0.2915131
## 5     7    0.4564548   0.4841492  2.783205e-04         0.4366629
## 6     8    0.5577898   0.5034417  5.362669e-03         0.4564548
```
---

## Predições

Plotando a predição
.pull-left[

```r
*plot(Predictions ~ Index,
     data = fits, type = "l", 
     col = "blue", lwd=3,
     xlab="Time", ylab="X")
*lines(Observations ~ Index,
      data = fits, 
      col=grey.colors(1, alpha=0.25), 
      lwd = 6)
legend("topright", 
       c("Observed", "Predicted"), 
       lty=1, lwd=c(6,3),
       col=c(grey.colors(1, alpha=0.25), 
             "blue"),bty="n")
```
]

.pull-right[
<img src="Day2_Simplex_projection_files/figure-html/unnamed-chunk-16-1.png" width="500" height="400" />
]
---
## Recapitulando

* Com a projeção **Simplex** podemos determinar a dimensão de **embedding** para reconstruir a dinâmica

* A dimensão será o máximo da correlação entre o predito e o observado, a predição será feita com uma projeção **Simplex**

* Com isso já podemos dar boas predições para o sistema
---
# Obrigado!

## Referências:

* Materiais e slides: [rafalopespx.github.io/WorkshopEDM/](http://rafalopespx.github.io/WorkshopEDM/)

* Canal do [Slack](https://app.slack.com/client/T01BJETR8S3/C01CXH8H9KM) para discussão, dúvidas, etc.

* Tutorial Hands-on Takens Theorem [Day 1](https://rafalopespx.github.io/WorkshopEDM/Hands-on_Takens.html)

* Tutorial Simplex projection made it simple [Day 2](https://rafalopespx.github.io/WorkshopEDM/simplex.html)